ЃgЃbЃvљiіwЃ[Ѓ~
ЊяЌКїДЂFќ{ЇZЂAЇпћеЇZЂ@Ђ@јаЅЖїДЂFЃOЃіЂ[ЃЊЃqЃІЇZ
ЊяЌКЈЌјqЉтЋЇЉ«ѓ╚ѓКЊ№іоњєіwјзї▒ЂEїДЌДЇ┼Јсѕ╩ЇѓЇZјзї▒ѓ╠љiіwЈm
ЊOњЖјwЊ▒ЂEјШІкѓ╔јЕљMѓаѓУЂEі«ЉSЈГљlљћљДЃNЃЅЃXЊ№іоЇZјзї▒љЖќтљiіwЈm
- ЂюѓКѓ╠ѓТѓцѓ╚ѓ▒ѓкѓ┼ѓЯѓеІCїyѓ╔ѓеќРѓбЇЄѓьѓ╣Ѕ║ѓ│ѓбЂB
- ЊdўbЂiЃtЃіЂ[Ѓ_ЃCЃёЃІЂjЂF0120-78-5878
сЃЌсЃГсѓ░сЃЕсЃЪсЃ│сѓ░ТЋЎт«ц
сѓ▓сѓ╣сЃѕсЃАсЃІсЃЦсЃ╝
сЃГсѓ░сѓцсЃ│
TIME
Ђ@
dai сЂЋсѓЊсЂ«ТЌЦУеў
2020
12Тюѕ
29
(уЂФ)
18:50
сЃѕсЃЃсЃЌсЂ«ТюгТБџсђютЁгт╝ЈсЂфсѓЊсЂдУдџсЂѕсЂфсЂёТќ╣сЂїсЂёсЂё
 тЅЇсЂ«ТЌЦУеў
ТгАсЂ«ТЌЦУеў
тЅЇсЂ«ТЌЦУеў
ТгАсЂ«ТЌЦУеў сѓФсЃєсѓ┤сЃфсЃ╝
сЂцсѓїсЂЦсѓї
сѓФсЃєсѓ┤сЃфсЃ╝
сЂцсѓїсЂЦсѓї
ТюгТќЄ
тЅЇтЏътйЊсЃќсЃГсѓ░сЂДу┤╣С╗ІсЂЌсЂЪС║гжЃйтцДтГд2011т╣┤ТќЄу│╗1уЋф(1)сЂ«тЋЈжАїсђЂТгАсЂ«сѓѕсЂєсЂФУДБсЂёсЂдсЂЇсЂЪуГћТАѕсЂїсЂѓсЂБсЂЪсђѓ
УДњсЂ«С║їуГЅтѕєуиџсЂ«ТђДУ│фсЂФсѓѕсѓі
AD^2№╝ЮAB├ЌACРѕњBD├ЌCD
сЂЊсѓїсЂФсѓѕсѓі
AD^2№╝Ю12├Ќ10Рѕњ6├Ќ5№╝Ю90
сѓѕсЂБсЂдAD=3Рѕџ10
сЂЮсѓЊсЂфтЁгт╝ЈсЂїсЂѓсЂБсЂЪсѓЊсЂІсђѓуЪЦсѓЅсѓЊсЂІсЂБсЂЪ№╝Ђ№╝ѕсЂЎсЂБсЂесЂ╝сЂЉ№╝Ѕ
сЂЊсЂ«ућЪтЙњсЂ«уГћТАѕсЂФсЂ»т«ЪсЂ»уХџсЂЇсЂїсЂѓсЂБсЂЪсђѓ
сђїсЂЊсЂ«ТђДУ│фсЂ»ТгАсЂ«сѓѕсЂєсЂФУе╝ТўјсЂДсЂЇсѓІсђѓ
Рќ│ABCсЂ«тцќТјЦтєєсѓњТЏИсЂЇуЏ┤уиџADсЂетєєсЂесЂ«С║цуѓ╣сѓњEсЂесЂЎсѓІсђѓ
РђдсђЇ
(С╗ЦСИІуЋЦ)
сЂЊсЂ«Уе╝ТўјсЂїт«ЪсЂФу┤аТЎ┤сѓЅсЂЌсЂІсЂБсЂЪ(УІЦт╣▓сѓ┐сѓцсЃЌсЃЪсѓ╣сЂїсЂѓсЂБсЂЪсЂїсђЂсЂесЂдсѓѓсѓѕсЂЈУђЃсЂѕсѓЅсѓїсЂдсЂёсЂЪ№╝Ѕсђѓ
сЂЌсЂЪсЂїсЂБсЂдсђЂС╗ітЏъсЂ«уГћТАѕсЂ«СИГсЂДТќЄтЈЦсЂфсЂЌсЂ«сЃЎсѓ╣сЃѕсѓбсЃ│сѓхсЃ╝№╝Ђ
сЂЙсЂѓсђЂУе╝ТўјсЂДсЂЇсѓІсѓЊсѓёсЂБсЂЪсѓЅсђЂсЂЮсЂ«Уе╝ТўјсЂ«УдЂжаўсЂДсЃђсѓцсЃгсѓ»сЃѕсЂФУДБсЂёсЂдсЂЈсѓїсѓїсЂ░сђЂсЂЮсѓїсЂДсѓѕсЂІсЂБсЂЪсЂ«сЂасЂЉсЂЕсђѓ№╝ѕСИђУѕгтїќсЂЎсѓІт┐ЁУдЂТђДсЂ»сЂЮсѓїсЂ╗сЂЕТёЪсЂўсЂфсЂёсђѓСй┐сЂёжЂЊсЂїуІГсЂёсЂЌ(Т│е1№╝Ѕ)
сЂЮсЂєсЂёсЂєТёЈтЉ│сЂДсЂ»сђЂтй╝сЂ«ТЈљтЄ║сЂЌсЂдсЂЈсѓїсЂЪУДБуГћсЂ»сђЂуДЂсЂ«ТЃ│т«џУДБсЂ«СИђсЂцсЂетЪ║ТюгуџёсЂФтљїсЂўсЂасЂБсЂЪсЂІсЂфсђѓ
уДЂсЂ«ТЃ│т«џУДБсЂЮсЂ«№╝Љ
РєЊсђђсђђсђђсђђсђђсђђсђђсђђсђђсђђсђђсђђсђђсђђсђђсђђРєЊ
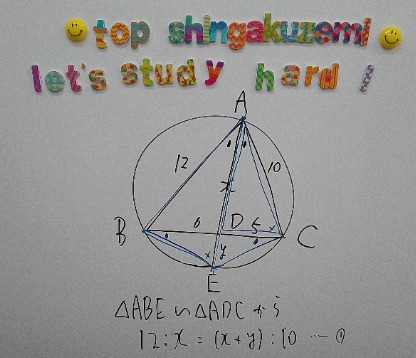
сЂЊсѓїсЂеТќ╣сЂ╣сЂЇсЂ«т«џуљєсЂФсѓѕсѓіxy=5├Ќ6сЂДсЂёсЂБсЂАсѓЄСИісЂїсѓісђѓ
С╗ќсЂФсЂ»сђЂAсЂІсѓЅBCсЂФтъѓуиџсѓњСИІсѓЇсЂЌсЂдСИЅт╣│Тќ╣сЂ«т«џуљєсѓњсѓѓсЂАсЂёсЂдADсЂФсЂцсЂёсЂдТќ╣уеІт╝ЈсѓњуФІсЂдсЂдсЂёсЂЪсѓѓсЂ«сЂїУдІсѓЅсѓїсЂЪсђѓ
№╝ѕсЂЊсЂБсЂАсЂїСИђуЋфсЂѓсѓісЂЮсЂєсЂфТЃ│т«џУДБсЂасЂеТђЮсЂБсЂдсЂёсЂЪсђѓУеўС║ІсЂ«уХџсЂЇсЂФсђїсЃўсЃГсЃ│сЂ«тЁгт╝ЈсѓњсђЂСИЅт╣│Тќ╣сЂ«т«џуљєсѓњућесЂёсЂдУе╝ТўјсђЇсЂесЂІТЏИсЂёсЂЪсЂЌ№╝Ѕ
тЅЇУђЁсЂ«сЂёсѓЈсЂ░сђїтЁгт╝ЈсђЇсђЂсЂЕсЂЊсЂІсЂДу┤╣С╗ІсЂЋсѓїсЂдсЂёсЂфсЂёсЂІсЂесѓ░сѓ░сЂБсЂдсЂ┐сЂЪсѓЅсђЂсЂ┐сЂцсЂЉсЂЪсђѓ
сђјжФўТаАТЋ░тГдсЂ«уЙјсЂЌсЂёуЅЕУфъсђЈсђђсЃъсѓ╣сѓфсђђсђђSB Creativeсђђсђђсђђсђђсђђсђђсђђсђђсђђсђђсђђ
тѕЮуЅѕ2016т╣┤1ТюѕсђѓУЉЌУђЁсЂ«сЃъсѓ╣сѓфсЂЋсѓЊсЂ»сЂЊсЂ«тЙїсѓѓтљїтљЇсЂ«сѓдсѓДсЃќсѓхсѓцсЃѕсЂДжФўТаАТЋ░тГдсЂ«тЪ║Тюгт«џуљєсЃ╗тЁгт╝ЈсЂІсѓЅтцДтГдТЋ░тГдсѓёТЋ░тГдсѓфсЃфсЃ│сЃћсЃЃсѓ»сЂ«УЕ▒жАїсЂЙсЂДсђЂсЂЋсЂЙсЂќсЂЙсЂфТЋ░тГдсЂФжќбсЂЎсѓІУѕѕтЉ│Ти▒сЂёУеўС║ІсѓњуЎ║С┐АсЂЋсѓїсЂдсЂёсѓІсђѓ
тєњжаГсЂ«тЁгт╝ЈсЂ»С╗іт╣┤уЎ║С┐АсЂ«УеўС║ІсђїУДњсЂ«С║їуГЅтѕєуиџсЂФжќбсЂЎсѓІ3сЂцсЂ«тЁгт╝ЈсђЇсЂ«3сЂцуЏ«сЂФу┤╣С╗ІсЂЋсѓїсЂдсЂёсѓІсђѓ
ТюгТЏИсЂ«СИГсЂДсЂёсЂАсЂ░сѓЊтЦйсЂЇсЂфУеўС║ІсЂ»
сђїТГБтцџжЮбСйЊсЂї5уе«жАъсЂЌсЂІсЂфсЂёсЂЊсЂесЂ«2жђџсѓісЂ«Уе╝ТўјсђЇ
сЂДсЂѓсѓІсђѓ
сѓфсѓцсЃЕсЃ╝сЂ«тцџжЮбСйЊт«џуљє(Т│е2)сЂІсѓЅсђЂТЋ┤ТЋ░тЋЈжАї№╝ѕтЏаТЋ░тѕєУДБсѓњућесЂёсѓІ№╝ЅсЂФТїЂсЂАУЙ╝сѓЊсЂДсЂёсѓІсЂесЂЊсѓЇсЂїуЅ╣сЂФсЂіТ░ЌсЂФтЁЦсѓісЂДсЂѓсѓІсђѓ
сЂЋсЂдсђЂТјѕТЦГсЂ«ТЎѓжќЊсђѓ
сђїТЋ░тГдсЂ«тІЅт╝исЂ»тЁгт╝ЈсѓњСИИТџЌУеўсЂЌсЂдсђЂсЂЊсѓїсѓњтЋЈжАїсЂФтйЊсЂдсЂ»сѓЂсѓІсЂЊсЂесђЇсЂесЂёсЂєТђЮсЂёУЙ╝сЂ┐сѓњТјњжЎцсЂЌсЂЪсЂёсђѓ
сђїТЋ░тГдсЂ«тІЅт╝исЂ»сђЂУЕдУАїжї»УфцсѓњжђџсЂўсЂдТЋ░сѓётЏ│тйбсЂ«ТђДУ│фсѓњуљєУДБсђЂт┐юућесЂЎсѓІсЂЊсЂесђЇсЂДсЂѓсѓІсђѓ
жђЪсЂЋсЂФ3сЂцсѓѓтЁгт╝ЈсЂ»сЂёсѓЅсЂфсЂёсђѓтЅ▓тљѕсЂФсЂцсЂёсЂдсѓѓ3сЂцсѓѓтЁгт╝ЈсЂ»сЂёсѓЅсЂфсЂёсђѓ
сЂЙсЂЌсЂдсЂЊсѓїсѓњСИђсЂцсЂФсЂЙсЂесѓЂсЂдсђїсЂ»сЂўсЂЇсђЇсђїсЂЈсѓѓсѓЈсђЇ№╝ѕсЃЏсЃЕсѓФсЃ│сѓ┐сЃ│сЃЄсѓисЃД№╝ЅсЂесЂІсЂёсЂєсЂ«сѓњТюђтѕЮсЂІсѓЅТЋЎсЂѕсѓІсЂ«сЂ»сђЂтГљсЂЕсѓѓсЂІсѓЅсђїТђЮУђЃсЂЌсЂдУЕдУАїсЂЌсЂдуљєУДБсЂЎсѓІсђЇТЕЪС╝џсѓњтЦфсЂєТюђСйјсЂ«сѓёсѓіТќ╣сЂасЂеТђЮсЂєсђѓ
сђї1тѕєсЂФ80mсЂ«сЃџсЃ╝сѓ╣сЂДТГЕсЂЈсЂесђЂ10тѕєсЂД800mсђЂ20тѕєсЂД1600mсђЂ60тѕєсЂасЂе4800mсђЂсЂцсЂЙсѓіТЎѓжђЪ4.8kmсђЇсЂесЂёсЂєсЂхсЂєсЂФсђЂУЄфтѕєсЂ«жаГсЂДУђЃсЂѕсЂдсЂёсЂЉсѓІсѓѕсЂєсЂФсЂЎсѓІсЂЊсЂесЂїсђїУђЃсЂѕсѓІтіЏсѓњУѓ▓сЂдсѓІсђЇсЂесЂёсЂєсЂЊсЂесЂДсЂ»сЂфсЂёсЂасѓЇсЂєсЂІсђѓ№╝ћ
сђїсЂ»сЂўсЂЇсђЇсЂ»тГљсЂЕсѓѓсЂїСй┐сЂБсЂдсЂёсѓІсЂ«сѓњтњјсѓЂсѓІсѓѓсЂ«сЂДсЂ»сЂфсЂёсЂїсђЂТЋЎсЂѕсѓІтЂ┤сЂїтѕЮсѓЂсЂІсѓЅсђїжђЪсЂЋсЂ«ТёЈтЉ│сђЇсѓњуљєУДБсЂЋсЂЏсѓІсЂЊсЂесѓњсЂѓсЂЇсѓЅсѓЂсЂдсђЂ
сђїсЂ»сЂўсЂЇсђЇсЂФтйЊсЂдсЂ»сѓЂсЂЪсѓЅуГћсЂѕсЂїтЄ║сѓІ(С╗ЦСИі№╝Ђ)сђѓсЃєсѓ╣сЃѕсЂДТ║ђуѓ╣сЂасЂІсѓЅсЂЊсЂ«тГљсЂ»сЂДсЂЇсѓІсѓѕсЂєсЂФсЂфсЂБсЂЪсЂЊсЂесЂФсЂЎсѓІ№╝Ђ
сЂесЂёсЂєсЂ«сЂ»сЂѓсЂЙсѓісЂФсѓѓС╣▒Тџ┤сЂфсѓёсѓіТќ╣сЂа(Т│е3)сђѓ
2020т╣┤сЂ»С╗ЦСИісЂДсЂЎсђѓ
2021т╣┤сЂ»ТўјсѓІсЂЈсђЂт«ЪсѓітцџсЂё1т╣┤сЂФсЂфсѓісЂЙсЂЎсѓѕсЂєсЂФсђѓ
ТюђтЙїсЂФ1тЋЈ№╝ѕСИђт┐юсђЂС╗іт╣┤т║дсЂ«СИГ3тљЉсЂЇсђѓТюЅтљЇтЋЈжАїсЂФсЂцсЂЇсЃЌсЃгсѓ╝сЃ│сЃѕсЂ»сЂѓсѓісЂЙсЂЏсѓЊ№╝Ѕ
сђї45├Ќ45сѓњУеѕу«ЌсЂЌсЂЪсЂєсЂѕсЂДсђЂсЂЮсЂ«ухљТъюсѓњтѕЕућесЂЌсЂд2021сѓњу┤атЏаТЋ░тѕєУДБсЂЌсЂфсЂЋсЂёсђЇ
Т│е1№╝џуДЂсЂ«сѓ»сЃЕсѓ╣сЂДсЂ»сђЂТЋ░тГдсЂ«ТЎѓжќЊсЂФсђїТ▒јућеТђДсЂїт░ЈсЂЋсЂёсђЇсЂесЂёсЂєУАеуЈЙсѓњсЂЌсЂЪсЂЊсЂесЂїсЂѓсѓісЂЙсЂЎсЂГсђѓ
Т│е2№╝џсђїсѓфсѓцсЃЕсЃ╝сЂ«тцџжЮбСйЊт«џуљєсђЇсЂесЂёсЂєтљЇтЅЇсЂ»сЂесѓѓсЂІсЂЈсђЂуЕ║жќЊтЏ│тйбсЂФжќбсЂЎсѓІсЂЊсЂ«ТђДУ│фсЂ»сђЂСИГ1сЂ«сЃєсѓГсѓ╣сЃѕсЂДу┤╣С╗ІсЂЌсЂдсЂёсѓІсѓѕсђѓ
Т│е3№╝џтЅ▓тљѕсѓёжђЪсЂЋсЂБсЂдсђЂућЪТ┤╗сЂ«СИГсЂДУЄфуёХсЂФУдџсЂѕсѓІсЂ«сЂїуљєТЃ│сЂДсЂЎсѓѕсЂГсђѓ
сђї5сЃЉсЃ╝сѓ╗сЃ│сЃѕт╝ЋсЂЇсЂфсЂ«сЂД60тєєт«ЅсЂЈсЂфсЂБсЂЪсђѓтЁЃсЂ«тђцТ«хсЂ»сЂёсЂЈсѓЅ№╝ЪсђЇсѓњсЂёсЂАсЂёсЂАсђїсЂЈсѓѓсѓЈсђЇсЂФсЂѓсЂдсЂ»сѓЂсЂдсђїт╝Ј№╝џ60├и0.05сђЇсЂесЂІсЂЌсЂфсЂёсЂДсЂЎсѓѕсЂГсђѓ
сђї10№╝ЁсЂД120тєєсђѓсЂасЂІсѓЅтЁЃсЂ«тђцТ«хсЂ»1200тєєсђЇсЂБсЂдсѓёсѓісЂЙсЂЎсѓѕсЂГсђѓ
УДњсЂ«С║їуГЅтѕєуиџсЂ«ТђДУ│фсЂФсѓѕсѓі
AD^2№╝ЮAB├ЌACРѕњBD├ЌCD
сЂЊсѓїсЂФсѓѕсѓі
AD^2№╝Ю12├Ќ10Рѕњ6├Ќ5№╝Ю90
сѓѕсЂБсЂдAD=3Рѕџ10
сЂЮсѓЊсЂфтЁгт╝ЈсЂїсЂѓсЂБсЂЪсѓЊсЂІсђѓуЪЦсѓЅсѓЊсЂІсЂБсЂЪ№╝Ђ№╝ѕсЂЎсЂБсЂесЂ╝сЂЉ№╝Ѕ
сЂЊсЂ«ућЪтЙњсЂ«уГћТАѕсЂФсЂ»т«ЪсЂ»уХџсЂЇсЂїсЂѓсЂБсЂЪсђѓ
сђїсЂЊсЂ«ТђДУ│фсЂ»ТгАсЂ«сѓѕсЂєсЂФУе╝ТўјсЂДсЂЇсѓІсђѓ
Рќ│ABCсЂ«тцќТјЦтєєсѓњТЏИсЂЇуЏ┤уиџADсЂетєєсЂесЂ«С║цуѓ╣сѓњEсЂесЂЎсѓІсђѓ
РђдсђЇ
(С╗ЦСИІуЋЦ)
сЂЊсЂ«Уе╝ТўјсЂїт«ЪсЂФу┤аТЎ┤сѓЅсЂЌсЂІсЂБсЂЪ(УІЦт╣▓сѓ┐сѓцсЃЌсЃЪсѓ╣сЂїсЂѓсЂБсЂЪсЂїсђЂсЂесЂдсѓѓсѓѕсЂЈУђЃсЂѕсѓЅсѓїсЂдсЂёсЂЪ№╝Ѕсђѓ
сЂЌсЂЪсЂїсЂБсЂдсђЂС╗ітЏъсЂ«уГћТАѕсЂ«СИГсЂДТќЄтЈЦсЂфсЂЌсЂ«сЃЎсѓ╣сЃѕсѓбсЃ│сѓхсЃ╝№╝Ђ
сЂЙсЂѓсђЂУе╝ТўјсЂДсЂЇсѓІсѓЊсѓёсЂБсЂЪсѓЅсђЂсЂЮсЂ«Уе╝ТўјсЂ«УдЂжаўсЂДсЃђсѓцсЃгсѓ»сЃѕсЂФУДБсЂёсЂдсЂЈсѓїсѓїсЂ░сђЂсЂЮсѓїсЂДсѓѕсЂІсЂБсЂЪсЂ«сЂасЂЉсЂЕсђѓ№╝ѕСИђУѕгтїќсЂЎсѓІт┐ЁУдЂТђДсЂ»сЂЮсѓїсЂ╗сЂЕТёЪсЂўсЂфсЂёсђѓСй┐сЂёжЂЊсЂїуІГсЂёсЂЌ(Т│е1№╝Ѕ)
сЂЮсЂєсЂёсЂєТёЈтЉ│сЂДсЂ»сђЂтй╝сЂ«ТЈљтЄ║сЂЌсЂдсЂЈсѓїсЂЪУДБуГћсЂ»сђЂуДЂсЂ«ТЃ│т«џУДБсЂ«СИђсЂцсЂетЪ║ТюгуџёсЂФтљїсЂўсЂасЂБсЂЪсЂІсЂфсђѓ
уДЂсЂ«ТЃ│т«џУДБсЂЮсЂ«№╝Љ
РєЊсђђсђђсђђсђђсђђсђђсђђсђђсђђсђђсђђсђђсђђсђђсђђсђђРєЊ
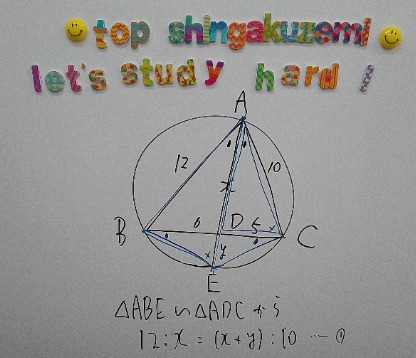
сЂЊсѓїсЂеТќ╣сЂ╣сЂЇсЂ«т«џуљєсЂФсѓѕсѓіxy=5├Ќ6сЂДсЂёсЂБсЂАсѓЄСИісЂїсѓісђѓ
С╗ќсЂФсЂ»сђЂAсЂІсѓЅBCсЂФтъѓуиџсѓњСИІсѓЇсЂЌсЂдСИЅт╣│Тќ╣сЂ«т«џуљєсѓњсѓѓсЂАсЂёсЂдADсЂФсЂцсЂёсЂдТќ╣уеІт╝ЈсѓњуФІсЂдсЂдсЂёсЂЪсѓѓсЂ«сЂїУдІсѓЅсѓїсЂЪсђѓ
№╝ѕсЂЊсЂБсЂАсЂїСИђуЋфсЂѓсѓісЂЮсЂєсЂфТЃ│т«џУДБсЂасЂеТђЮсЂБсЂдсЂёсЂЪсђѓУеўС║ІсЂ«уХџсЂЇсЂФсђїсЃўсЃГсЃ│сЂ«тЁгт╝ЈсѓњсђЂСИЅт╣│Тќ╣сЂ«т«џуљєсѓњућесЂёсЂдУе╝ТўјсђЇсЂесЂІТЏИсЂёсЂЪсЂЌ№╝Ѕ
тЅЇУђЁсЂ«сЂёсѓЈсЂ░сђїтЁгт╝ЈсђЇсђЂсЂЕсЂЊсЂІсЂДу┤╣С╗ІсЂЋсѓїсЂдсЂёсЂфсЂёсЂІсЂесѓ░сѓ░сЂБсЂдсЂ┐сЂЪсѓЅсђЂсЂ┐сЂцсЂЉсЂЪсђѓ
сђјжФўТаАТЋ░тГдсЂ«уЙјсЂЌсЂёуЅЕУфъсђЈсђђсЃъсѓ╣сѓфсђђсђђSB Creativeсђђсђђсђђсђђсђђсђђсђђсђђсђђсђђсђђ
тѕЮуЅѕ2016т╣┤1ТюѕсђѓУЉЌУђЁсЂ«сЃъсѓ╣сѓфсЂЋсѓЊсЂ»сЂЊсЂ«тЙїсѓѓтљїтљЇсЂ«сѓдсѓДсЃќсѓхсѓцсЃѕсЂДжФўТаАТЋ░тГдсЂ«тЪ║Тюгт«џуљєсЃ╗тЁгт╝ЈсЂІсѓЅтцДтГдТЋ░тГдсѓёТЋ░тГдсѓфсЃфсЃ│сЃћсЃЃсѓ»сЂ«УЕ▒жАїсЂЙсЂДсђЂсЂЋсЂЙсЂќсЂЙсЂфТЋ░тГдсЂФжќбсЂЎсѓІУѕѕтЉ│Ти▒сЂёУеўС║ІсѓњуЎ║С┐АсЂЋсѓїсЂдсЂёсѓІсђѓ
тєњжаГсЂ«тЁгт╝ЈсЂ»С╗іт╣┤уЎ║С┐АсЂ«УеўС║ІсђїУДњсЂ«С║їуГЅтѕєуиџсЂФжќбсЂЎсѓІ3сЂцсЂ«тЁгт╝ЈсђЇсЂ«3сЂцуЏ«сЂФу┤╣С╗ІсЂЋсѓїсЂдсЂёсѓІсђѓ
ТюгТЏИсЂ«СИГсЂДсЂёсЂАсЂ░сѓЊтЦйсЂЇсЂфУеўС║ІсЂ»
сђїТГБтцџжЮбСйЊсЂї5уе«жАъсЂЌсЂІсЂфсЂёсЂЊсЂесЂ«2жђџсѓісЂ«Уе╝ТўјсђЇ
сЂДсЂѓсѓІсђѓ
сѓфсѓцсЃЕсЃ╝сЂ«тцџжЮбСйЊт«џуљє(Т│е2)сЂІсѓЅсђЂТЋ┤ТЋ░тЋЈжАї№╝ѕтЏаТЋ░тѕєУДБсѓњућесЂёсѓІ№╝ЅсЂФТїЂсЂАУЙ╝сѓЊсЂДсЂёсѓІсЂесЂЊсѓЇсЂїуЅ╣сЂФсЂіТ░ЌсЂФтЁЦсѓісЂДсЂѓсѓІсђѓ
сЂЋсЂдсђЂТјѕТЦГсЂ«ТЎѓжќЊсђѓ
сђїТЋ░тГдсЂ«тІЅт╝исЂ»тЁгт╝ЈсѓњСИИТџЌУеўсЂЌсЂдсђЂсЂЊсѓїсѓњтЋЈжАїсЂФтйЊсЂдсЂ»сѓЂсѓІсЂЊсЂесђЇсЂесЂёсЂєТђЮсЂёУЙ╝сЂ┐сѓњТјњжЎцсЂЌсЂЪсЂёсђѓ
сђїТЋ░тГдсЂ«тІЅт╝исЂ»сђЂУЕдУАїжї»УфцсѓњжђџсЂўсЂдТЋ░сѓётЏ│тйбсЂ«ТђДУ│фсѓњуљєУДБсђЂт┐юућесЂЎсѓІсЂЊсЂесђЇсЂДсЂѓсѓІсђѓ
жђЪсЂЋсЂФ3сЂцсѓѓтЁгт╝ЈсЂ»сЂёсѓЅсЂфсЂёсђѓтЅ▓тљѕсЂФсЂцсЂёсЂдсѓѓ3сЂцсѓѓтЁгт╝ЈсЂ»сЂёсѓЅсЂфсЂёсђѓ
сЂЙсЂЌсЂдсЂЊсѓїсѓњСИђсЂцсЂФсЂЙсЂесѓЂсЂдсђїсЂ»сЂўсЂЇсђЇсђїсЂЈсѓѓсѓЈсђЇ№╝ѕсЃЏсЃЕсѓФсЃ│сѓ┐сЃ│сЃЄсѓисЃД№╝ЅсЂесЂІсЂёсЂєсЂ«сѓњТюђтѕЮсЂІсѓЅТЋЎсЂѕсѓІсЂ«сЂ»сђЂтГљсЂЕсѓѓсЂІсѓЅсђїТђЮУђЃсЂЌсЂдУЕдУАїсЂЌсЂдуљєУДБсЂЎсѓІсђЇТЕЪС╝џсѓњтЦфсЂєТюђСйјсЂ«сѓёсѓіТќ╣сЂасЂеТђЮсЂєсђѓ
сђї1тѕєсЂФ80mсЂ«сЃџсЃ╝сѓ╣сЂДТГЕсЂЈсЂесђЂ10тѕєсЂД800mсђЂ20тѕєсЂД1600mсђЂ60тѕєсЂасЂе4800mсђЂсЂцсЂЙсѓіТЎѓжђЪ4.8kmсђЇсЂесЂёсЂєсЂхсЂєсЂФсђЂУЄфтѕєсЂ«жаГсЂДУђЃсЂѕсЂдсЂёсЂЉсѓІсѓѕсЂєсЂФсЂЎсѓІсЂЊсЂесЂїсђїУђЃсЂѕсѓІтіЏсѓњУѓ▓сЂдсѓІсђЇсЂесЂёсЂєсЂЊсЂесЂДсЂ»сЂфсЂёсЂасѓЇсЂєсЂІсђѓ№╝ћ
сђїсЂ»сЂўсЂЇсђЇсЂ»тГљсЂЕсѓѓсЂїСй┐сЂБсЂдсЂёсѓІсЂ«сѓњтњјсѓЂсѓІсѓѓсЂ«сЂДсЂ»сЂфсЂёсЂїсђЂТЋЎсЂѕсѓІтЂ┤сЂїтѕЮсѓЂсЂІсѓЅсђїжђЪсЂЋсЂ«ТёЈтЉ│сђЇсѓњуљєУДБсЂЋсЂЏсѓІсЂЊсЂесѓњсЂѓсЂЇсѓЅсѓЂсЂдсђЂ
сђїсЂ»сЂўсЂЇсђЇсЂФтйЊсЂдсЂ»сѓЂсЂЪсѓЅуГћсЂѕсЂїтЄ║сѓІ(С╗ЦСИі№╝Ђ)сђѓсЃєсѓ╣сЃѕсЂДТ║ђуѓ╣сЂасЂІсѓЅсЂЊсЂ«тГљсЂ»сЂДсЂЇсѓІсѓѕсЂєсЂФсЂфсЂБсЂЪсЂЊсЂесЂФсЂЎсѓІ№╝Ђ
сЂесЂёсЂєсЂ«сЂ»сЂѓсЂЙсѓісЂФсѓѓС╣▒Тџ┤сЂфсѓёсѓіТќ╣сЂа(Т│е3)сђѓ
2020т╣┤сЂ»С╗ЦСИісЂДсЂЎсђѓ
2021т╣┤сЂ»ТўјсѓІсЂЈсђЂт«ЪсѓітцџсЂё1т╣┤сЂФсЂфсѓісЂЙсЂЎсѓѕсЂєсЂФсђѓ
ТюђтЙїсЂФ1тЋЈ№╝ѕСИђт┐юсђЂС╗іт╣┤т║дсЂ«СИГ3тљЉсЂЇсђѓТюЅтљЇтЋЈжАїсЂФсЂцсЂЇсЃЌсЃгсѓ╝сЃ│сЃѕсЂ»сЂѓсѓісЂЙсЂЏсѓЊ№╝Ѕ
сђї45├Ќ45сѓњУеѕу«ЌсЂЌсЂЪсЂєсЂѕсЂДсђЂсЂЮсЂ«ухљТъюсѓњтѕЕућесЂЌсЂд2021сѓњу┤атЏаТЋ░тѕєУДБсЂЌсЂфсЂЋсЂёсђЇ
Т│е1№╝џуДЂсЂ«сѓ»сЃЕсѓ╣сЂДсЂ»сђЂТЋ░тГдсЂ«ТЎѓжќЊсЂФсђїТ▒јућеТђДсЂїт░ЈсЂЋсЂёсђЇсЂесЂёсЂєУАеуЈЙсѓњсЂЌсЂЪсЂЊсЂесЂїсЂѓсѓісЂЙсЂЎсЂГсђѓ
Т│е2№╝џсђїсѓфсѓцсЃЕсЃ╝сЂ«тцџжЮбСйЊт«џуљєсђЇсЂесЂёсЂєтљЇтЅЇсЂ»сЂесѓѓсЂІсЂЈсђЂуЕ║жќЊтЏ│тйбсЂФжќбсЂЎсѓІсЂЊсЂ«ТђДУ│фсЂ»сђЂСИГ1сЂ«сЃєсѓГсѓ╣сЃѕсЂДу┤╣С╗ІсЂЌсЂдсЂёсѓІсѓѕсђѓ
Т│е3№╝џтЅ▓тљѕсѓёжђЪсЂЋсЂБсЂдсђЂућЪТ┤╗сЂ«СИГсЂДУЄфуёХсЂФУдџсЂѕсѓІсЂ«сЂїуљєТЃ│сЂДсЂЎсѓѕсЂГсђѓ
сђї5сЃЉсЃ╝сѓ╗сЃ│сЃѕт╝ЋсЂЇсЂфсЂ«сЂД60тєєт«ЅсЂЈсЂфсЂБсЂЪсђѓтЁЃсЂ«тђцТ«хсЂ»сЂёсЂЈсѓЅ№╝ЪсђЇсѓњсЂёсЂАсЂёсЂАсђїсЂЈсѓѓсѓЈсђЇсЂФсЂѓсЂдсЂ»сѓЂсЂдсђїт╝Ј№╝џ60├и0.05сђЇсЂесЂІсЂЌсЂфсЂёсЂДсЂЎсѓѕсЂГсђѓ
сђї10№╝ЁсЂД120тєєсђѓсЂасЂІсѓЅтЁЃсЂ«тђцТ«хсЂ»1200тєєсђЇсЂБсЂдсѓёсѓісЂЙсЂЎсѓѕсЂГсђѓ
жќ▓УдД(4565)
| сѓ│сЃАсЃ│сЃѕсѓњТЏИсЂЈ |
|---|
|
сѓ│сЃАсЃ│сЃѕсѓњТЏИсЂЈсЂФсЂ»сЃГсѓ░сѓцсЃ│сЂїт┐ЁУдЂсЂДсЂЎсђѓ |
| «тЅЇсЂ«ТюѕТгАсЂ«Тюѕ» | ||||||
| ТЌЦ | Тюѕ | уЂФ | Т░┤ | Тюе | жЄЉ | тюЪ |
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 | ||
сѓФсЃєсѓ┤сЃфсЃ╝
ТюђУ┐ЉсЂ«ТЌЦУеў
- жФўТаАжЃесѓисЃЕсЃљсѓ╣сЂћТАѕтєЁ№╝ѕТўЦТюЪУгЏу┐њТюЪжќЊ№╝Ѕ
- жФўТаАтЁЦтГдсЂЙсЂДсЂФсѓёсЂБсЂдсЂісЂЇсЂЪсЂёсЂЊсЂе№╝ѕ2025Тћ╣УеѓуЅѕ№╝Ѕ
- daiсЂ«тЁЦУЕдтЋЈжАїуаћуЕХРђЋС╗цтњї№╝Ќт╣┤т║дТ╗ІУ│ђуюїуФІжФўТаАтЁЦУЕдсЂФсЂцсЂёсЂд№╝ѕтЇ│ТЌЦуЅѕ№╝Ѕ
- сЃѕсЃЃсЃЌсЂ«ТюгТБџРђЋТіђсѓњсЂёсЂБсЂ▒сЂёуЪЦсЂБсЂдсЂдсѓѓСй┐сЂѕсЂфсЂЇсѓЃТёЈтЉ│сЂїуёАсЂё
- GHТаАжФўТаАжЃесђђСйЊжеЊТјѕТЦГсЂ«сЂћТАѕтєЁ
- сЃѕсЃЃсЃЌсЂ«ТюгТБџРђЋтЏйУфъсѓњС╝ИсЂ░сЂЌсЂЪсЂЉсѓїсЂ░УІ▒Уфъсѓњсѓёсѓї
- сЃѕсЃЃсЃЌсЂ«ТюгТБџРђЋуДЉтГдсЂежЮъуДЉтГд№╝ѕтєЇУфГ№╝Ѕ
ТюђУ┐ЉсЂ«сѓ│сЃАсЃ│сЃѕ
- RE: daiсЂ«тЁЦУЕдтЋЈжАїуаћуЕХVol26. dai [05-08 22:34]
- RE: daiсЂ«тЋЈжАїуаћуЕХVol.16РђЋУЕд dai [03-06 15:08]
- RE: сЃѕсЃЃсЃЌсЂ«ТюгТБџРђЋ№╝ЋТќЄтГЌсЂДуЎЙС║║СИђждќ dai [07-06 22:41]
тљёТюѕсЂ«ТЌЦУеў
- 2025т╣┤03Тюѕ (3)
- 2025т╣┤02Тюѕ (4)
- 2025т╣┤01Тюѕ (3)
- 2024т╣┤12Тюѕ (2)
- 2024т╣┤11Тюѕ (2)
- 2024т╣┤10Тюѕ (4)
- 2024т╣┤09Тюѕ (2)
- 2024т╣┤08Тюѕ (1)
- 2024т╣┤07Тюѕ (3)
- 2024т╣┤06Тюѕ (3)
- 2024т╣┤05Тюѕ (4)
- 2024т╣┤04Тюѕ (3)

