ГgГbГvРiКwГ[Г~
УёЧ«МІБFЦ{НZБAНЎФ®НZБ@Б@О†ЙкМІБFГOГКБ[ГУГqГЛНZ
УёЧ«ПЧОqСеХНс»«УпК÷ТЖКwОуМ±БEМІЧІН≈ПгИ НВНZОуМ±ВћРiКwПm
УOТкОwУ±БEОцЛ∆В…О©РMВ†ВиБEКЃСSП≠РlРФРІГNГЙГXУпК÷НZОуМ±РкЦеРiКwПm
- БЬ«žВ槻±В∆В≈ВаВ®ЛCМyВ…В®ЦвВҐНЗВнВєЙЇВ≥ВҐБB
- УdШbБiГtГКБ[Г_ГCГДГЛБjБF0120-78-5878
гГЧгГ≠гВ∞гГ©гГЯгГ≥гВ∞жХЩеЃ§
гВ≤гВєгГИгГ°гГЛгГ•гГЉ
гГ≠гВ∞гВ§гГ≥
TIME
Б@
dai гБХгВУгБЃжЧ•и®Ш
2020
11жЬИ
18
(ж∞і)
16:51
гГИгГГгГЧгБЃжЬђж£ЪгАЬгАМгБѓгБШгБНгАНгАМгБПгВВгВПгАНгБЃдљХгБМгБДгБСгБ™гБДгБЃгБЛгАВ
 еЙНгБЃжЧ•и®Ш
жђ°гБЃжЧ•и®Ш
еЙНгБЃжЧ•и®Ш
жђ°гБЃжЧ•и®Ш гВЂгГЖгВігГ™гГЉ
гБ§гВМгБ•гВМ
гВЂгГЖгВігГ™гГЉ
гБ§гВМгБ•гВМ
жЬђжЦЗ
е§ЪгБПгБЃе≠РгБ©гВВгБѓгАБйАЯгБХгВДеЙ≤еРИгБЂгБ§гБДгБ¶гАБзі†жЬігБ™жДЯи¶ЪгВТжМБгБ£гБ¶гБДгВЛгВВгБЃгБІгБВгВЛгАВ
гБЯгБ®гБИгБ∞гАБ50гГ°гГЉгГИгГЂгВТ9зІТгБІиµ∞гВЛе≠РгБ®8зІТгБІиµ∞гВЛе≠РгБѓгБ©гБ°гВЙгБМйАЯгБДгБЛгВПгБЛгВЙгБ™гБДе≠РгБѓгБДгБ™гБДгБЧгАБгАМеАНгАНгБ®гБЛгАМеНКеИЖгАНгБ®гБЛгБДгБЖжДЯи¶ЪгБМгВПгБЛгВЙгБ™гБДе∞Пе≠¶зФЯгВВгБїгБ®гВУгБ©гБДгБ™гБДгБ†гВНгБЖгАВ
гБЭгБЃзі†жЬігБ™жДЯи¶ЪгВТиВ≤гБ¶гВЛгБУгБ®гВТжФЊж£ДгБЧгБ¶гАБгАМжДПеС≥гБ™гБ©иАГгБИгБ™гБПгБ¶гВИгБДгБЛгВЙгБ®гБЂгБЛгБПеЕђеЉПгБЂељУгБ¶гБѓгВБгБ¶ж≠£гБЧгБДз≠ФгБИгВТжЫЄгБНгБ™гБХгБДгАВгАНгБ®гБЩгВЛгБ®гАБе≠РгБ©гВВгБѓиАГгБИгВЛгБУгБ®гВТгВДгВБгБ¶гБЧгБЊгБЖгАВгБ§гБЊгВКгАБгВҐгГЫгБЂгБ™гВЛгБЃгБІгБВгВЛгАВ
гБВгВЛз®ЛеЇ¶зЃЧжХ∞гБМгБІгБНгВЛгБ®и¶ЛгБИгВЛе≠РгБЂгАБйБУзРЖгВТжХЩгБИгВЛеЙНгБЂгАМгБѓгБШгБНгАНгБЂељУгБ¶гБѓгВБгВЛгБУгБ®гБ†гБСжХЩгБИиЊЉгВАгАВдЄАи¶ЛгАМгБѓгБШгБНгАНгБѓз∞°еНШгБ™гБЃгБІгАБгБЭгБЃе≠РгБѓгАМйАЯгБХгБ™гВУгБ¶з∞°еНШгБ†гАНгБ®жАЭгБ£гБ¶гБЧгБЊгБЖгБ†гВНгБЖпЉИгБїгВУгБ®гБЖгБѓгАБгБВгВЛз®ЛеЇ¶и≥ҐгБДе≠РгБ©гВВгБѓгАМгБѓгБШгБНгАНгБ™гБ©зЯ•гВЙгБ™гБПгБ¶гВВгАМйАЯгБХгАНгБЃж¶ВењµиЗ™дљУгБѓгБЭгВУгБ™гБЂйЫ£гБЧгБДгБУгБ®гБІгБѓгБ™гБДгБѓгБЪгБ†пЉЙгАВгБЯгБЧгБЛгБЂгВЂгГ©гГЉгГЖгВєгГИгБѓдљЩи£ХгБЃ100зВєгАВ
гБЧгБЛгБЧгБЭгВУгБ™е≠РгБЃжЬЂиЈѓгБѓжВ≤жГ®гБ™гВВгБЃгБЂгБ™гВЛгБ†гВНгБЖгАВгБЭгБЃе≠РгБЂдЄ≠е≠¶еПЧй®УгВТгБХгБЫгБЯгБ®гБЧгБ¶гАБдїХдЇЛзЃЧгАБжЧЕдЇЇзЃЧгБ™гБ©гБЃењЬзФ®еХПй°МгБѓи®АгБЖгБЂеПКгБ∞гБЪгАБеХПй°МжЦЗгБЃи°®зПЊгВТгБ°гВЗгБ£гБ®е§ЙгБИгБЯгБ†гБСгБЃжЩЃйАЪгБЃйАЯгБХгБЃеХПй°МгБІгБЩгВЙгАБеЕ®гБПгБІгБНгБ™гБПгБ¶гБЛгВПгБДгБЭгБЖгБ™зЫЃгБЂеРИгВПгБЫгВЛгБУгБ®гБЂгБ™гВЛгБ†гВНгБЖгАВдЄ≠е≠¶еПЧй®УгВТгБЧгБ™гБЛгБ£гБЯгБ®гБЧгБ¶гВВгАБдЄ≠е≠¶гБЂдЄКгБМгБ£гБ¶гБЛгВЙзЙєгБЂзРЖзІСгБІгБДгВНгБДгВНгБ™еНШдљНељУгБЯгВКзЪДгБ™ж¶ВењµпЉИеѓЖеЇ¶гАБйЫїж∞ЧжКµжКЧгАБеЬІеКЫгБ™гБ©пЉЙгБМгБІгБ¶гБНгБ¶гАБгБЭгБЃгБЯгБ≥гБЂгГЖгГ≥гГИгВ¶гГ†гВЈпЉИж≥®1пЉЙгВТдљЬгБ£гБ¶жХЩгБИгБ¶гВДгВЙгБ™гБДгБ®еЕ®гБПеХПй°МгБМиІ£гБСгБ™гБДгАБгБ®гБДгБЖгБУгБ®гБЂгБ™гБ£гБ¶гБЧгБЊгБЖгБЃгБІгБВгВЛгАВ
гБДгБСгБ™гБДгАВгБ§гБДзЖ±гБПгБ™гБ£гБ¶гБЧгБЊгБ£гБЯпЉИгБ™гВУгБЛи¶ЛгБЯпЉЙгАВ
ж∞ЧгВТеПЦгВКзЫігБЧгБ¶гАБжђ°гБЃжЬђгВТгБ©гБЖгБЮгАБ( ^-^)_жЧ¶~
гАОдЄ≠е≠¶гБЃзЯ•и≠ШгБІгВ™гВ§гГ©гГЉгБЃеЕђеЉПгБМгВПгБЛгВЛгАПгААйИіжЬ®и≤Ђе§™йГОгААеЕЙжЦЗз§ЊжЦ∞жЫЄ
дЇМжђ°жЦєз®ЛеЉПгБМиІ£гБСгВЛгБУгБ®гАБгГФгВњгВігГ©гВєгБЃеЃЪзРЖгВТзЯ•гБ£гБ¶гБДгВЛгБУгБ®гВТгВВгБ£гБ¶гАБгАМдЄ≠е≠¶гБЃзЯ•и≠ШгБІгАНгБ®гБДгБ£гБ¶гВИгБДгБ†гВНгБЖгАВжЬђжЫЄгВТи™≠з†ігБЩгВЛгБЯгВБгБЃжЬАдљОйЩРгБЃзЯ•и≠ШгБѓгБУгВМгБПгВЙгБДгАВ
гБЭгБУгБЛгВЙгВєгВњгГЉгГИгБЧгБ¶гАБжЬАзµВзЪДгБЂeгБЃiѕАдєЧгБМ-1гБЂгБ™гВЛгБ®гБДгБЖгВ™гВ§гГ©гГЉгБЃеЕђеЉПгБЃзРЖиІ£гВТзЫЃжМЗгБЩгАВйАФдЄ≠гБЂењЕи¶БгБ™дЄЙиІТжѓФпЉИsin,cos)гВДеѓЊжХ∞пЉИlogпЉЙгАБиЗ™зДґеѓЊжХ∞гБЃеЇХeгБЃеЃЪзЊ©гБ™гБ©гАБењЕи¶БгБ™жХ∞еЉПгБЃзРЖиІ£гБЃгБЯгВБгБЃиІ£и™ђеЛХзФїпЉИYou Tube)гВВеВЩгБИгВЙгВМгБ¶гБДгВЛгАВ
й°ЮжЫЄпЉИгБ®гБДгБЖгБЛгБУгБЃгГЖгГЉгГЮгБЃжЬђгБ®гБЧгБ¶гБѓгБЪгБ£гБ®еЕИзЩЇгБ†гБМпЉЙгГИгГГгГЧгБЃжЬђж£ЪгБЂгБѓгАБгАОгВ™гВ§гГ©гГЉгБЃиіИгВКзЙ©гАПпЉИеРЙзФ∞ж≠¶гААгБ°гБПгБЊе≠¶иКЄжЦЗеЇЂпЉЙгВВзљЃгБДгБ¶гБВгВЛгАВгБЯгБ†гБЧгВИгБїгБ©гБЃжХ∞еЉЈгБІгБ™гБДйЩРгВКгАБдЄ≠е≠¶зФЯгБЂгБ®гБ£гБ¶гАОгВ™гВ§гГ©гГЉгБЃиіИгВКзЙ©гАПгБѓгБ°гВЗгБ£гБ®иНЈгБМйЗНгБЛгВНгБЖгАВгБЭгВМгБЂжѓФгБєгВЛгБ®гАБжЬђжЫЄгБѓгБЪгБДгБґгВУгБ®гБ£гБ§гБНгВДгБЩгБПгБ™гБ£гБ¶гБДгВЛгАВгБ™гБКгАБжХ∞е≠¶гВђвИТвА¶пЉИж≥®2пЉЙ
еŕ詶гБМжЧ©гБПзµВгВПгБ£гБЯпЉИзЙєиЙ≤гАБзІБзЂЛе∞Вй°ШгБ™гБ©пЉЙдЄ≠3зФЯгБЂгБКгБЩгБЩгВБгБЧгБЯгБДгАВ
и≤Ђе§™йГОеЕИзФЯгБМдЄНеЃЪжЬЯгБЂеЗЇгБЧгБ¶жЭ•гВЙгВМгВЛжХіжХ∞еХПй°МгБЃеЛХзФїпЉИе§Іе≠¶еŕ詶еХПй°МгБМгГ°гВ§гГ≥пЉЙгВВгБКгБЩгБЩгВБгАВпЉИж≥®3пЉЙ
гБХгБ¶гАБжОИж•≠гБЃжЩВйЦУгБ†гАВ
дїКеЫЮгБѓгАБгБВгВЛеЫ≥嚥гБЃжАІи≥™гБЂгБ§гБДгБ¶гБЃжОИж•≠гВТдЄАйГ®еЕђйЦЛгБЧгВИгБЖгАВ
11жЬИеЃЯжЦљгБЃжїЛи≥АVгВВгБЧгБЃжХ∞е≠¶гБІгАБгБ®гБВгВЛжЬЙеРНеХПй°МгБМеЗЇй°МгБХгВМгБ¶гБДгБЯгАВгАМеє≥и°МеЫЫ茯嚥гААйЫ£иІТеХПй°МгАНгБІж§Ь糥гБЩгВЛгБ®гБЩгБРгБЂи¶ЛгБ§гБЛгВЛеХПй°МгБІгБВгВЛгАВ
вЖУгААгААгААгААгААгААгААгААгААгААгААгААгААгААгААвЖУ
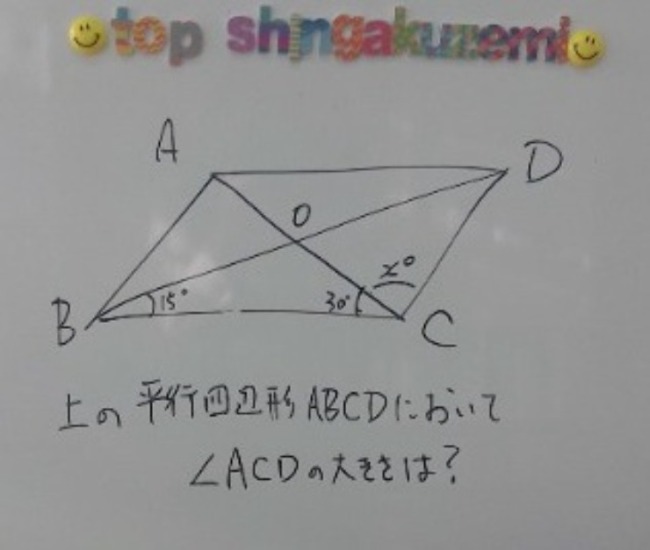
гГОгГЉгГТгГ≥гГИгБ†гБ®гБНгБ§гБДгБСгВМгБ©гАБ殰詶гБЃеХПй°МгБЂгБѓи™Ше∞ОгБМгБ§гБДгБ¶гБДгВЛгБЃгБІгАБж≠£иІ£гБЊгБІгБЯгБ©гВКзЭАгБСгБЯдЇЇгБѓжХ∞гГСгГЉгВїгГ≥гГИз®ЛеЇ¶гБДгБЭгБЖгАВпЉИж≥®4гБЂз≠ФгБИгВТжЫЄгБНгБЊгБЧгБЯпЉЙ
еРМгБШзЩЇжГ≥гБѓжђ°гБЃгВИгБЖгБ™еХПй°МгБЂгВВйБ©зФ®гБІгБНгВЛгБ†гВНгБЖгАВпЉИзЃЧжХ∞жШЯдЇЇгБХгВУгБЃйЫ£йЦҐдЄ≠е≠¶еПЧй®УзФЯеРСгБСгБЃгАМеЫ≥嚥гГЙгГ™гГЂгАНгБЛгВЙпЉЙ
вЖУгААгААгААгААгААгААгААгААгААгААгААгААгААгААвЖУ
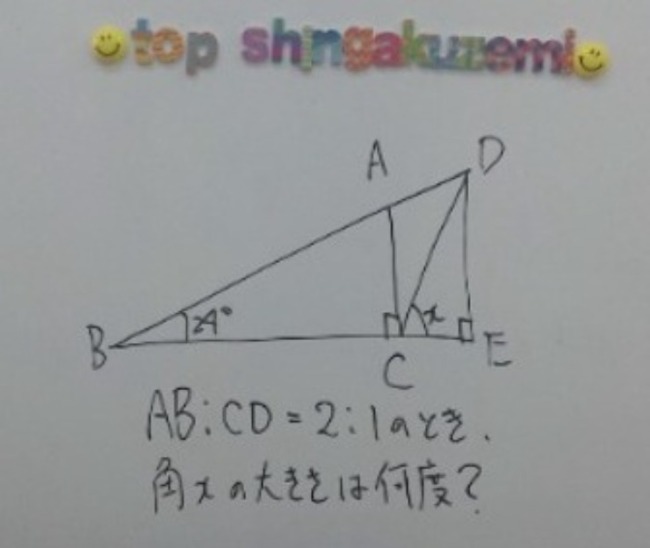
пЉИж≥®5гБЂз≠ФгБИгБЃгБњжЫЄгБНгБЊгБЧгБЯпЉЙ
гБВгВЛгБДгБѓгБУгВМгАВпЉИеП§еЕЄгБ®гБДгБЖгБєгБНжЯРеЫ≥嚥еХПй°МйЫЖпЉИе§ІгБНгБ™жЫЄеЇЧгБ™гВЙе£≤гБ£гБ¶гБДгВЛгААж≥®6пЉЙгБЛгВЙпЉЙ
вЖУгААгААгААгААгААгААгААгААгААгААгААгААгААгААвЖУ
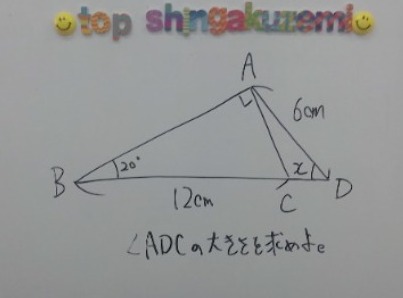
пЉИж≥®7гБЂз≠ФгБИгБЃгБњжЫЄгБНгБЊгБЧгБЯпЉЙ
дї•дЄКгБЂеЕ±йАЪгБЩгВЛзЩЇжГ≥гБѓгАБйХЈжֺ嚥гВТеѓЊиІТзЈЪгБІеИЗгВЛгБУгБ®гБЂгВИгБ£гБ¶зРЖиІ£гБІгБНгВЛгБ†гВНгБЖгАВ
вЖУгААгААгААгААгААгААгААгААгААгААгААгААгААгААвЖУ

(жЬђгБЃеЖЕеЃєгБѓжЬђй°МгБ®гБВгБЊгВКйЦҐдњВгБВгВКгБЊгБЫгВУпЉЙ
гБУгБЃжІЛеЫ≥пЉИгВҐгВ§гГЗгВҐпЉЙгБѓжМБгБ£гБ¶гБКгБПгБ®гБИгБИгВИгАВ
гАМеЫ≥嚥еХПй°МгБІеЫ∞гБ£гБЯгВЙдЇМз≠ЙиЊЇдЄЙиІТ嚥гВТжОҐгБЫгАНгБѓжКШгБЂиІ¶гВМгБ¶жОИж•≠гБІгБКи©±гБЧгБЧгБ¶гБДгВЛгБУгБ®гВДгБ≠гАВ
жЬђжЧ•гБѓдї•дЄКпЉБпЉБ
ж≥®1пЉЪгАМгБЧгБњгБЯгАНгАМйЫїйЫїйЫїгАНпЉИгГНгВњгБІгБЩгВИпЉЙгАМгБ°гБВгВБгАН(пЉЯ)гАВгГЖгГ≥гГИгВ¶гГ†гВЈгВТжЫЄгБДгБ¶дЄЄжЪЧи®ШгБЩгВЛгВЙгБЧгБДгАВз©ґж•µгБѓгАМгГҐгГЂгВ∞гГ™гВ≥гАНпЉИж∞ЧгБЂгБ™гВЛжЦєгБѓгАБж§Ь糥гБСгВУгБХгБПгБЕгАЬпЉЙгАВ
ж≥®2пЉЪгАМжХ∞е≠¶гВђгГЉгГЂгАНгБЂи®АеПКгБЧгВИгБЖгБ®жАЭгБ£гБЯгБМгАБгВ™гВ§гГ©гГЉгБЃеЕђеЉПгБѓжЙ±гВПгВМгБ¶гБДгБ™гБЛгБ£гБЯгБ≠гАВгАМжХ∞е≠¶гВђгГЉгГЂгАНгБѓгГХгВІгГЂгГЮгГЉгБЃжЬАзµВеЃЪзРЖгБМзІАйАЄгАВгВµгВ§гГҐгГ≥гВЈгГ≥гБЃгГЙгВ≠гГ•гГ°гГ≥гВњгГ™пЉИжЦ∞жљЃжЦЗеЇЂгАБгБУгБ°гВЙгВВгГИгГГгГЧгБЃGHж†°жЬђж£ЪгБЂгБВгВЛпЉЙгБ†гБСгБІгБѓгБНгБ§гБДгБСгБ©гАБ2еЖКгВТзґЪгБСгБ¶и™≠гВБгБ∞ж•љгБЧгБДгАВ
ж≥®3пЉЪгБУгВМгВТжЫЄгБДгБ¶гБДгБЯељУжЧ•гБЃжЬЭгБЂгАМ11пЉЊ3пЉЛ397гААгВТзі†еЫ†жХ∞еИЖиІ£гБЧгВНгАНгБ®гБДгБЖеХПй°МгБМжµБгВМгБ¶гБНгБЯгАВйЭҐзЩљгБЛгБ£гБЯгБСгВМгБ©пЉИ2жЧ•гБІ2дЄЗеЫЮдї•дЄКеЖНзФЯгБХгВМгБ¶гБДгВЛпЉБпЉЙгАБдЄЙдєЧгБЃе±ХйЦЛгВДеЉПгБЃйЩ§ж≥ХгБ®дљЩгВКгВТиАГгБИгБ¶гБФгВЙгВУгАБгБ®гБДгБЖиґ£жЧ®гБ†гВНгБЖгБЛгВЙгАБдЄАиИђгБЃеЕђзЂЛдЄ≠е≠¶зФЯгБЂгБѓгБ°гВЗгБ£гБ®вА¶пЉИдЄ≠йЂШдЄАи≤Ђж†°гБЃдЄ≠3зФЯгБ™гВЙиИИеС≥жЈ±гБПи¶ЛгВМгБЭгБЖпЉЙ
ж≥®4пЉЪ105еЇ¶гАВAгБЛгВЙBCгБЂеЮВзЈЪгВТгБКгВНгБЧгАБгБЭгБЃиґ≥гВТEгБ®гБЧгВИгБЖгАВ
гААгААгААгБЩгВЛгБ®гАБAO=CO=EOгАБвИ†CAE=60еЇ¶
гБХгВЙгБЂBEпЉЭAEгБМи¶ЛгБИгВЛгБ≠гАВ
ж≥®5пЉЪ72еЇ¶
ж≥®6пЉЪгАМйЂШж†°гБЄгБЃжХ∞е≠¶гААзЫЃгБІиІ£гБПеєЊдљХгААзЫізЈЪеЫ≥嚥磮гАНжЭ±дЇђеЗЇзЙИ
ж≥®7пЉЪ40еЇ¶
йЦ≤и¶І(7307)
| гВ≥гГ°гГ≥гГИгВТжЫЄгБП |
|---|
|
гВ≥гГ°гГ≥гГИгВТжЫЄгБПгБЂгБѓгГ≠гВ∞гВ§гГ≥гБМењЕи¶БгБІгБЩгАВ |
| «еЙНгБЃжЬИжђ°гБЃжЬИ» | ||||||
| жЧ• | жЬИ | зБЂ | ж∞і | жЬ® | йЗС | еЬЯ |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | |||||
гВЂгГЖгВігГ™гГЉ
жЬАињСгБЃжЧ•и®Ш
- гГИгГГгГЧгБЃжЬђж£ЪвАХе∞ПеЄВж∞Сзђђ2жЬЯ
- гГИгГГгГЧгБЃжЬђж£ЪвАХгБХгБПгВЙ
- йЂШж†°йГ®гВЈгГ©гГРгВєгБФж°ИеЖЕпЉИжШ•жЬЯиђЫзњТжЬЯйЦУпЉЙ
- йЂШж†°еЕ•е≠¶гБЊгБІгБЂгВДгБ£гБ¶гБКгБНгБЯгБДгБУгБ®пЉИ2025жФєи®ВзЙИпЉЙ
- daiгБЃеŕ詶еХПй°Мз†Фз©ґвАХдї§еТМпЉЧеєіеЇ¶жїЛи≥АзЬМзЂЛйЂШж†°еŕ詶гБЂгБ§гБДгБ¶пЉИеН≥жЧ•зЙИпЉЙ
- гГИгГГгГЧгБЃжЬђж£ЪвАХжКАгВТгБДгБ£гБ±гБДзЯ•гБ£гБ¶гБ¶гВВдљњгБИгБ™гБНгВГжДПеС≥гБМзД°гБД
- GHж†°йЂШж†°йГ®гААдљУй®УжОИж•≠гБЃгБФж°ИеЖЕ
жЬАињСгБЃгВ≥гГ°гГ≥гГИ
- RE: daiгБЃеŕ詶еХПй°Мз†Фз©ґVol26. dai [05-08 22:34]
- RE: daiгБЃеХПй°Мз†Фз©ґVol.16вАХ詶 dai [03-06 15:08]
- RE: гГИгГГгГЧгБЃжЬђж£ЪвАХпЉХжЦЗе≠ЧгБІзЩЊдЇЇдЄАй¶Ц dai [07-06 22:41]
еРДжЬИгБЃжЧ•и®Ш
- 2025еєі04жЬИ (2)
- 2025еєі03жЬИ (3)
- 2025еєі02жЬИ (4)
- 2025еєі01жЬИ (3)
- 2024еєі12жЬИ (2)
- 2024еєі11жЬИ (2)
- 2024еєі10жЬИ (4)
- 2024еєі09жЬИ (2)
- 2024еєі08жЬИ (1)
- 2024еєі07жЬИ (3)
- 2024еєі06жЬИ (3)
- 2024еєі05жЬИ (4)

