ГgГbГvРiКwГ[Г~
УёЧ«МІБFЦ{НZБAНЎФ®НZБ@Б@О†ЙкМІБFГOГКБ[ГУГqГЛНZ
УёЧ«ПЧОqСеХНс»«УпК÷ТЖКwОуМ±БEМІЧІН≈ПгИ НВНZОуМ±ВћРiКwПm
УOТкОwУ±БEОцЛ∆В…О©РMВ†ВиБEКЃСSП≠РlРФРІГNГЙГXУпК÷НZОуМ±РкЦеРiКwПm
- БЬ«žВ槻±В∆В≈ВаВ®ЛCМyВ…В®ЦвВҐНЗВнВєЙЇВ≥ВҐБB
- УdШbБiГtГКБ[Г_ГCГДГЛБjБF0120-78-5878
гГЧгГ≠гВ∞гГ©гГЯгГ≥гВ∞жХЩеЃ§
гВ≤гВєгГИгГ°гГЛгГ•гГЉ
гГ≠гВ∞гВ§гГ≥
TIME
Б@
dai гБХгВУгБЃжЧ•и®Ш
2020
10жЬИ
21
(ж∞і)
16:25
гГИгГГгГЧгБЃжЬђж£ЪвАХдЄЙиІТ嚥гБЃйЭҐз©НжѓФгБ®зЫЄдЉЉ
 еЙНгБЃжЧ•и®Ш
жђ°гБЃжЧ•и®Ш
еЙНгБЃжЧ•и®Ш
жђ°гБЃжЧ•и®Ш гВЂгГЖгВігГ™гГЉ
жЧ•еЄЄ
гВЂгГЖгВігГ™гГЉ
жЧ•еЄЄ
жЬђжЦЗ
гАМеРЫгБЃгГЙгГЂгГБгВІгВҐгГ≥гГЙгВђгГГгГРгГЉгГКгАНгВТеЉХгБНеРИгБДгБЂеЗЇгБЩгБЊгБІгВВгБ™гБПгАБгБЂгБКгБДгБ®гБДгБЖгВВгБЃгБѓи®ШжЖґгБ®еИЖгБЛгБ°гБМгБЯгБПзµРгБ≥гБ§гБДгБ¶гБДгВЛгАВ
гАОеЉЈйБЛгБЃжМБгБ°дЄїгАПгААзАђе∞ЊгБЊгБДгБУгААжЦЗжШ•жЦЗеЇЂгААгААгААгААгААгААгАА
еЕГеЦґж•≠иБЈOLгБМеН†гБДеЄЂгБЂиїҐиБЈгБЧгАБгВЈгГІгГГгГФгГ≥гВ∞гВїгГ≥гВњгГЉгБЃзЙЗйЪЕгБІжВ©гБњгВТжК±гБИгВЛдЇЇгБЃиГМдЄ≠гВТжКЉгБЩзЙ©и™ЮгАВзЯ≠зЈ®4гБ§гАВ
гБ≤гБ®гБ§зЫЃгБЃгАМгГЛгГЩгВҐгАНгБІгБѓе∞Пе≠¶зФЯгБЃе∞СеєігБМзЫЄиЂЗгБЂи®™гВМгВЛгАВе∞СеєігБЃзȴ趙гВТжАЭгБЖж∞ЧжМБгБ°гБ®зȴ趙гБМе∞СеєігБЃж∞ЧжМБгБ°гВТж°ИгБШгВЛж∞ЧжМБгБ°гАБгБЭгВМгВЙгБМи™≠иАЕгБЃжГ≥еГПгВТиґЕгБИгБ¶гБВгБЯгБЯгБЛгБДгАВ
жДЯжґЩењЕиЗ≥гБ†гБМгАБзЯ≠зЈ®е∞Пи™ђгБѓдЄАи©±гВТдЄАж∞ЧгБЂи™≠гБЊгБ™гБДгБ®гВВгБ£гБЯгБДгБ™гБДгБ≠(еПНзЬБ)гАВ
йАФдЄ≠гБІжЧ•гВТз©ЇгБСгБ¶гБЧгБЊгБЖгБ®гАБгБЫгБ£гБЛгБПеЉµгБ£гБ¶гБВгБ£гБЯдЉПзЈЪгВТењШгВМгБ¶гБЧгБЊгБЖгАВ
гБХгБ¶гАБжОИж•≠гБЃжЩВйЦУгБ†гАВжЙЛгВТзљЃгБДгБ¶гБЊгБ£гБЩгБРеЙНгВТеРСгБДгБ¶гБПгБ†гБХгБДгАВгБУгВУгБ∞гВУгВПпЉБ
9жЬИгБЃеНКгБ∞гБЂдљЬжИРгБЧгБЯдЄ≠3з§ЊдЉЪгБЃзҐЇи™НгГЖгВєгГИгБЂгАБжђ°гБЃеХПй°МгВТеЕ•гВМгБ¶гБКгБДгБЯгАВ
жђ°гБЃжЦЗзЂ†дЄ≠гБЃпЉИгААпЉЙеЖЕгБЃи™ЮеП•гБЂгБ§гБДгБ¶гАБж≠£гБЧгБСгВМгБ∞гАЗгВТгАБ虧гБ£гБ¶гБДгВМгБ∞ж≠£гБЧгБДи™ЮеП•гВТжЫЄгБНгБ™гБХгБДгАВ
гАМ2020еєі9жЬИ16жЧ•гВИгВК3жЧ•йЦУгБЃдЉЪжЬЯгБІпЉИиЗ®жЩВеЫљдЉЪпЉЙгБМйЦЛгБЛгВМгАБи°Жи≠∞йЩҐжЬђдЉЪи≠∞гБЂгБКгБДгБ¶иПЕзЊ©еБЙеЖЕйЦ£еЃШжИњйХЈеЃШгБМжђ°гБЃзЈПзРЖе§ІиЗ£гБЂпЉИдїїеСљпЉЙгБХгВМгБЯгАВгАН
еЃЪжЬЯ詶й®УгБЃжЧ•з®ЛгБЃйГљеРИгБІгБУгБЃгГЖгВєгГИгВТеЃЯжЦљгБЧгБЯгБЃгБМ10жЬИ2йА±зЫЃгБЂгБЪгВМгБУгВУгБІгБЧгБЊгБ£гБЯгБЃгБМжЃЛењµгБ†гБМгАБзµРжЮЬзЪДгБЂзµ±ж≤їж©ЯжІЛгБЃгВИгБДеЊ©зњТгБЂгБ™гБ£гБЯгБЃгБІгБѓгБ™гБДгБЛгБ®жАЭгБЖгАВ
ж°ИгБЃеЃЪгАБгАМиЗ®жЩВеЫљдЉЪгАНгВТгАМзЙєеИ•еЫљдЉЪгАНгБ®жЫЄгБНжПЫгБИгБ¶гБДгВЛз≠Фж°ИгБМгБ°гВЙгБїгВЙи¶ЛгВЙгВМгБЯгАВ
еЊМиАЕгБЃгАМдїїеСљгАНгБѓгБїгБ®гВУгБ©гБЃзФЯеЊТгБМгАМжМЗеРНгАНгБЂжЫЄгБНжПЫгБИгВЛгБУгБ®гБМгБІгБНгБ¶гБДгБЯгАВ
з≠ФгБИеРИгВПгБЫгБЃжЩВгБЂ
гАМгБВгАБгБЧгБЊгБ£гБЯгАВзЙєеИ•еЫљдЉЪгБѓи°Жи≠∞йЩҐгБЃиІ£жХ£гБЃгБВгБ®гВДгБ£гБЯгАВгАН
гБ™гВУгБ¶зЩЇи®АгБМеЗЇгБ¶гБДгБ¶гАБдЄАеЃЙењГпЉИгВИгБКгВПгБЛгБ£гБ¶гБДгВЛгВДгБ™гБДгБЛгАЬпЉЙгАВ
дЄ≠3жХ∞е≠¶гБІгАМзЫЄдЉЉгАНгБЂгБ§гБДгБ¶е≠¶зњТгАВдїКеєігБѓйЭҐз©НжѓФгБЃжОИж•≠гБЃгБ®гБНгАБгГЖгВ≠гВєгГИгБЃдЊЛй°МгБЂи°МгБПеЙНгБЂгБѓгБШгВБгБЂжђ°гБЃеХПй°МгВТжПРз§ЇгБЧгБ¶гБњгБЯгАВ
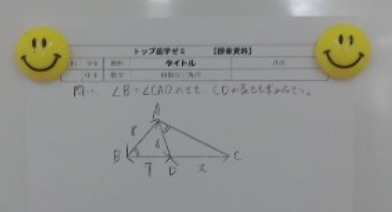
пЉИеИґйЩРжЩВйЦУ3еИЖгАВжАЭгБДгБ§гБДгБЯгБУгБ®гВТгБ®гВКгБВгБИгБЪгВДгБ£гБ¶гБњгБ¶пЉЙ
иІ£и™ђгБѓгБУгБЃдЄЛгБЂ
гААвЖУ
гААвЖУ
гААвЖУ
гААвЖУ
гААвЖУ
гБЊгБВгАБгБВгВЛз®ЛеЇ¶иЇЂгБЂгБ§гБДгБ¶гБДгВЛе≠РгБ™гВЙвЦ≥ABCгБ®вЦ≥DACгБЃзЫЄдЉЉгБМгБЩгБРгБЂи¶ЛгБИгВЛгБ†гВНгБЖгБЛгВЙгАБгБЭгБЃеЕИгБ©гБЖгБЩгВЛгБЃгБЛгБМи¶ЛгБЯгБЛгБ£гБЯгБЃгБІгБВгВЛгАВ
зІБгБЃжДПеЫ≥гБѓгАБ
гАМзЫЄдЉЉжѓФ4:3гБМи¶ЛгБИгВЛгБСгВМгБ©гБЭгБ£гБЛгВЙеЕИдЄКжЙЛгБДгБУгБ®гБДгБЛгВУгВИгБ≠гБИгАН
гБ®и®АгБ£гБ¶гАБз۪䊊嚥гБЃйЭҐз©НжѓФгАБйЂШгБХеЕ±йАЪгБЃдЄЙиІТ嚥гБЃйЭҐз©НжѓФгБЃи©±гБЂи°МгБНгБЯгБЛгБ£гБЯгВПгБСгБІгБВгВЛгАВ
гБ®гБУгВНгБМгБ©гБ£гБУгБДгАБCAгБЃйХЈгБХгВТпљЩгБ®гБІгВВзљЃгБДгБ¶жѓФдЊЛеЉПгВТдЇМжЬђгАБдЄКжЙЛгБДгБУгБ®зЂЛгБ¶гВМгБ∞гАБйА£зЂЛжЦєз®ЛеЉПгБІCDгБЃйХЈгБХгБМж±ВгБЊгБ£гБ¶гБЧгБЊгБЖпЉИе§Ъе∞СзЕ©йЫСгБ†гБСгБ©пЉЙгАВзµДгБњеРИгВПгБЫгБХгБИйБЄгБєгБ∞дЇМжђ°жЦєз®ЛеЉПгБЂгБЩгВЙгБ™гВЙгБ™гБДгАВ
гВДгБ£гБ¶гБДгВЛйАФдЄ≠гБЂж∞ЧгБ•гБДгБЯгБМжОИж•≠гБѓгВВгБЖиµ∞гВКеЗЇгБЧгБ¶гБДгБ¶еЊМгБЃз•≠гВКгАВ
жђ°гБЃиІ£гБНжЦєгБЃйЃЃгВДгБЛгБХгБЂжДПи≠ШгБМи°МгБ£гБ¶гБЧгБЊгБДгАБз≠ЦгБЂжЇЇгВМгБЯжДЯгБМжЛ≠гБИгБ™гБДгАВ
иІ£
вЦ≥ABCгБ®вЦ≥DACгБЃзЫЄдЉЉжѓФгБМ4:3гБ†гБЛгВЙйЭҐз©НжѓФгБѓ16:9гАВ
гБЩгВЛгБ®вЦ≥ABDгБ®вЦ≥ADCгБЃйЭҐз©НжѓФгБѓ7:9
й†ВзВєгВТеЕ±жЬЙгБЩгВЛдЄЙиІТ嚥гБЃйЭҐз©НгБЃжѓФгБѓеЇХиЊЇгБЃжѓФгБЂз≠ЙгБЧгБДгБЛгВЙ
BD=7гБ™гВЙCD=9гАВ
дї•дЄКгАВ
гБЊгБВгАБиЊЇгБЃжѓФгВДйЂШгБХгБЃжѓФгБ®йЭҐз©НжѓФгБЃеЗЇгБЧеЕ•гВМгБѓгБІгБНгВЛгВИгБЖгБЂгБ™гБ£гБ¶гБКгБПгБ®гБДгВНгБДгВНдЊњеИ©гБ†гБЛгВЙпЉИж≥®1пЉЙгАБгБУгБЃж©ЯдЉЪгБЂиЇЂгБЂгБ§гБСгБ¶гВВгВЙгБИгБ∞гБЭгВМгБІгВИгБЧгАВ
жЬђжЧ•гБЃжОИж•≠гБѓгБУгБУгБЊгБІгАВ
еЃњй°МгБ®гБЧгБ¶гГЖгВ≠гВєгГИp114гБЃ1зХ™гБЛгВЙp115гБЃ5зХ™гБЊгБІгВДгБ£гБ¶гБњгБ¶гБ≠гАВгГЖгВєгГИгБІгБІгБНгБ™гБЛгБ£гБЯеХПй°МгБѓгБУгБЃеЊМиІ£гБНгБ™гБКгБЧгБ¶зІБгБЃгБ®гБУгВНгБЂжМБгБ£гБ¶гБНгБ¶гАВ
гБЭгВМгБШгВГгАБиІ£жХ£пЉБ
ж≥®1пЉЪдЄЙиІТ嚥гБЂгБ§гБДгБ¶гАБгБУгБЖгБДгБ£гБЯиЊЇгБЃжѓФгВДйЂШгБХгБЃжѓФгБ®йЭҐз©НжѓФгБЃгАМеЗЇгБЧеЕ•гВМгАНгБѓгАБйЫ£йЦҐйЂШж†°еŕ詶пЉИгБ®гБПгБЂйЦҐжХ∞гБ®гБЃиЮНеРИеХПй°МгБІгБњгВЙгВМгВЛпЉЙгБѓгВВгБ°гВНгВУгАБйЫ£йЦҐдЄ≠е≠¶еŕ詶гБІгВВењЕй†ИпЉИгВАгБЧгВНдЄ≠е≠¶еŕ詶гБІгБѓгАБињСеєігАМгГЩгГ≥гГДеИЗгВКгАНгБ®гБЛгБДгБ£гБ¶гГЭгГФгГ•гГ©гГЉгБЂгБ™гБ£гБ¶гБНгБ¶гБДгВЛгБњгБЯгБДпЉЙгАВ
дЄ≠е≠¶ж†°гБЃжХЩзІСжЫЄгБІгБѓдЄ≠2гБІгАМйЭҐз©НгБЃз≠ЙгБЧгБДдЄЙиІТ嚥гАНгБ®гБДгБЖгБКй°МгБІгБ°гВЗгВНгБ£гБ®гВДгВЛгБ†гБСгВДгВВгВУгБ≠гАВ
йЦ≤и¶І(7830)
| гВ≥гГ°гГ≥гГИгВТжЫЄгБП |
|---|
|
гВ≥гГ°гГ≥гГИгВТжЫЄгБПгБЂгБѓгГ≠гВ∞гВ§гГ≥гБМењЕи¶БгБІгБЩгАВ |
| «еЙНгБЃжЬИжђ°гБЃжЬИ» | ||||||
| жЧ• | жЬИ | зБЂ | ж∞і | жЬ® | йЗС | еЬЯ |
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
гВЂгГЖгВігГ™гГЉ
жЬАињСгБЃжЧ•и®Ш
- гГИгГГгГЧгБЃжЬђж£ЪвАХе∞ПеЄВж∞Сзђђ2жЬЯ
- гГИгГГгГЧгБЃжЬђж£ЪвАХгБХгБПгВЙ
- йЂШж†°йГ®гВЈгГ©гГРгВєгБФж°ИеЖЕпЉИжШ•жЬЯиђЫзњТжЬЯйЦУпЉЙ
- йЂШж†°еЕ•е≠¶гБЊгБІгБЂгВДгБ£гБ¶гБКгБНгБЯгБДгБУгБ®пЉИ2025жФєи®ВзЙИпЉЙ
- daiгБЃеŕ詶еХПй°Мз†Фз©ґвАХдї§еТМпЉЧеєіеЇ¶жїЛи≥АзЬМзЂЛйЂШж†°еŕ詶гБЂгБ§гБДгБ¶пЉИеН≥жЧ•зЙИпЉЙ
- гГИгГГгГЧгБЃжЬђж£ЪвАХжКАгВТгБДгБ£гБ±гБДзЯ•гБ£гБ¶гБ¶гВВдљњгБИгБ™гБНгВГжДПеС≥гБМзД°гБД
- GHж†°йЂШж†°йГ®гААдљУй®УжОИж•≠гБЃгБФж°ИеЖЕ
жЬАињСгБЃгВ≥гГ°гГ≥гГИ
- RE: daiгБЃеŕ詶еХПй°Мз†Фз©ґVol26. dai [05-08 22:34]
- RE: daiгБЃеХПй°Мз†Фз©ґVol.16вАХ詶 dai [03-06 15:08]
- RE: гГИгГГгГЧгБЃжЬђж£ЪвАХпЉХжЦЗе≠ЧгБІзЩЊдЇЇдЄАй¶Ц dai [07-06 22:41]
еРДжЬИгБЃжЧ•и®Ш
- 2025еєі04жЬИ (2)
- 2025еєі03жЬИ (3)
- 2025еєі02жЬИ (4)
- 2025еєі01жЬИ (3)
- 2024еєі12жЬИ (2)
- 2024еєі11жЬИ (2)
- 2024еєі10жЬИ (4)
- 2024еєі09жЬИ (2)
- 2024еєі08жЬИ (1)
- 2024еєі07жЬИ (3)
- 2024еєі06жЬИ (3)
- 2024еєі05жЬИ (4)

